An RV-6A owner contacted me Friday wondering about how to take cruise speed vs power data from one altitude and correct them to a different altitude. He wants to produce the data for a series of cruise performance tables for a wide range of altitudes, then do a small test program to validate them. He wondered if he could make use of the rule of thumb that speed varies with the cube root of power. I sent him a long response, and an Excel spreadsheet, but I figured that some other people might be interested in this topic too.
I'll offer two approaches - one that is simple, and probably not so accurate, and a more complex, but more accurate one.
Simple Approach - Assume Constant Cd
The simple approach is similar to the cube root rule of thumb. It assumes that the drag coefficient does not change. This is OK for small corrections, but it won't work very well for large corrections.
We could use existing perf data (from Van's or the CAFE Foundation), use an assumed propeller efficiency, and calculate a drag coefficient. Then, we assume that the prop efficiency and drag coefficient do not change, and calculate the TAS at some other condition. This is simple, but it is probably not that accurate, as in fact the drag coefficient and prop efficiency will change as we change condition.
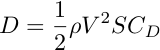
where:
D = drag![]() = air density
= air density
V = True Air Speed
S = wing area
CD = drag coefficient
Power required = drag times speed. And the power produced = engine power times prop efficiency. So:
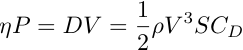
where:![]() = propeller efficiency
= propeller efficiency
P = engine power
From this we get:
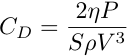
and:
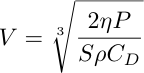
The air density at sea level standard day = 0.0023769 slugs / ft^3
The air density at some other altitude, assuming standard temperature, = sea level density times the density ratio.
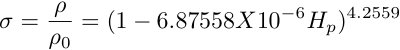
where:![]() = density ratio
= density ratio![]() = density at sea level on standard day = 0.0023769 slugs / ft^3
= density at sea level on standard day = 0.0023769 slugs / ft^3
Hp = pressure altitude
I've put together an Excel spreadsheet does the above calculations.
More Complex Approach - Cd Changes With Speed
A more accurate approach would account for the way that Cd changes with speed. The two largest components of drag are profile drag and induced drag. At low speed, induced drag dominates, and at high speed profile drag dominates. The drag coefficient for profile drag is constant. But the drag coefficient for induced drag is a function of the lift coefficient.
![]()
where:
CDi = drag coefficient for induced drag
CDp = drag coefficient for profile drag
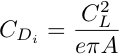
where:
CL = lift coefficient
e = Oswald's span efficiency![]() = 3.14159...
= 3.14159...
A = aspect ratio = wing span / average wing chord
In 1 g flight, the lift equals the weight. So,
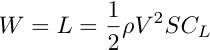
where:
W = weight
L = lift

Using all the above, if we have values for the drag coefficient for profile drag, and Oswald's span efficiency, we can calculate more accurate values for Cd. The CAFE Foundation Aircraft Performance report for the RV-6A has values for Oswald's span efficiency and the drag coefficient for profile drag. They instrumented the aircraft with a device to measure the longitudinal movement of the crankshaft in the thrust bearing, and used this to set the throttle to get zero thrust, and then did glide testing to measure drag at different speeds. Their value of 0.851 for the span efficiency should be a good guess for all the short wing RVs. Their value of 0.0211 for the profile drag coefficient is probably valid for RV-6A only. You can tweak this value very slightly for other models to get a better match on max speed.
The Excel spreadsheet also calculates power required using this approach.
Propeller Efficiency
Propeller efficiency varies depending on airspeed, altitude, rpm, power, etc. If a correction is made over a small range of airspeeds, altitude or power, it is reasonable to assume the prop efficiency remains constant. But, if there is a significant change in condition there will probably be a change in prop efficiency. If the prop is being operated near its design point, he efficiency will probably be somewhere between 80% and 85%, depending on the prop blade thickness and the skill of the designer. Metal prop blades can be quite thin, so their efficiency should be near the top end of this range. Wooden or composite props have thicker blades, and thus the efficiency will be near the lower end of this range. If the condition is significantly away from the design point, the prop efficiency could be 5% to 10% lower.