The basic method as described by Lycoming assumes the rpm is the same with mixture for peak EGT as it is at the fuel flow of interest. Thus the method, as described, is only workable for a constant speed prop, as the rpm will vary with fuel flow if you have a fixed pitch prop. I created a hypothetical extension to Lycoming’s method, that assumes that fuel flow will vary linearly with rpm for small changes of rpm at a constant MP, altitude and mixture control position. So, for example, if we have 2500 rpm and 10 gph at peak EGT, and 9 gph and 2400 rpm at the fuel flow of interest, I assume that if you could keep rpm constant, the fuel flow at peak EGT at 2400 rpm would be = 10 * 2400/2500 = 9.6 gph. Given that this calculation method is much less sensitive to errors in fuel flow at peak EGT as it is to fuel flows at the test condition, I think this approach will work for fixed pitch props.
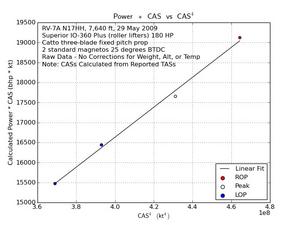
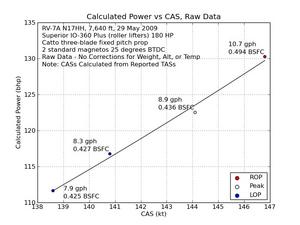
I got some more power from fuel flow data today - this data was from Howard Handelman’s RV-7A with “Superior IO-360 Plus (roller lifters) 180 HP”, two mags and a Catto three blade fixed pitch prop. He got me four different fuel flows at about 2500 rpm at 7600 ft - one pretty close to peak power rich of peak EGT, and one at peak EGT and two more lean of peak EGT. I ran the data through the Lycoming power from fuel flow method, with the hypothetical addition to the method to make it work for fixed pitch prop. The variation of speed vs calculated power looks very good, which suggests that this power calculation method provides powers that vary correctly with fuel flow. If you look at the plot of Calculated Power vs CAS, you’ll see that all four points are very, very close to the line of perfect fit. This suggests that this method does a pretty good job of handling the differences in specific fuel consumption between rich of peak and lean of peak ops.
It is too early to declare victory yet, but the first two results are encouraging. Note: I don’t yet have a very good idea as to whether this method accurately calculates power. At the moment my investigation has focused on whether it provides a calculated power that varies correctly as the mixture varies. The question of whether it provides the correct power value is a more difficult one to answer. I hope to eventually have enough data to be able to compare the power values from the classical Lycoming power charts. But even that will not provide a definitive answer, as there are so few of our engines actually match a configuration that was delivered by Lycoming, so it is hard to find a good power chart to use for every engine.
Thanks Howard.